• 第七章 狄克斯特拉算法
  • 步骤
  • 例子
  • 限制
  • 补充
  • 小结
  • 疑问
  • 书籍纠错

狄克斯特拉算法————寻找加权图中最短路径的算法。

第七章 狄克斯特拉算法

寻找加权图（带有权重的图）中最短路径的算法。

步骤

• 书中：
  1. 找出最便宜节点，即可在最短时间内抵达的节点；
  2. 更新该节点的邻居的开销；
  3. 重复这个过程，直到对图中每个节点都这么做；
  4. 计算最终路径； 这个步骤说明并不是很清晰。
• 实际运用：
  下方权重值皆为从起点到当前节点的权重值之和。

1. 列出除起点外的所有节点；
2. 对节点添加权重值，其中起点直接指向的节点的权重是能直接列出的，其他节点可列为∞（无穷）；
3. 找到目前权重最小的节点，重复步骤2，即列出此节点指向节点的权重（需途径当前节点），若已有权重，则与当前权重比较取较小值并更新，同时将当前节点标记为已操作。
4. 找到目前未操作的权重最小的节点，重复上述步骤；
5. 所有节点操作完毕后，即可得到达到终点的最小权重。
6. 路径怎么找呢，在上述添加个更新权重的时候，应该记录到达此节点的上一个节点是谁，那么从终点向上即可得到当前的最短路径。

例子

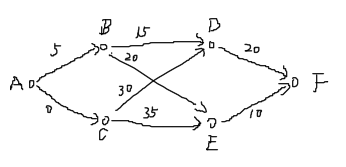
表格中双波浪线为删除

1. 列出所有节点

   节点	起点至权重	上级节点	已操作
   B
   C
   D
   E
   F

2. 添加权重

   节点	起点至权重	上级节点	已操作
   B	5	A
   C	0	A
   D	∞
   E	∞
   F	∞

3. 获取当前权重最小节点C，更新此节点的邻居节点的权重值。 即A->C->D:30、A->C->E:35，需经过B。 更新上级节点和将C标记为已操作

   节点	起点至权重	上级节点	已操作
   B	5	A	√
   C	0	A
   D	30	C
   E	35	C
   F	∞

4. 获取当前未操作的权重最小节点B，重复步骤3，发现此时A->B->D权重为5+15=20，A->B->E权重为5+20=25，都比已记录的DE权重小，需更新DE数据和DE上级节点。

   节点	起点至权重	上级节点	已操作
   B	5	A	√
   C	0	A	√
   D	30 20	C B
   E	35 25	C B
   F	∞

5. 重复此步骤至除终点外所有节点都被操作获得：

   节点	起点至权重	上级节点	已操作
   B	5	A	√
   C	0	A	√
   D	20	B	√
   E	25	B	√
   F	35	E

所以最短路线为A->B->E->F，最小权重为35。

限制

狄克斯特拉算法有一个使用限制，当存在负权边时会有问题，所以不适用负权边存在的情况。 可以尝试添加B->C为-7权重，此时操作完C后再操作B，C的权重会变成最小，而C已被标记为已操作，会有冲突。可使用贝尔曼-福特算法，没看。

补充

其基本原理是：每次新扩展一个距离最短的点，更新与其相邻的点的距离。当所有边权都为正时，由于不会存在一个距离更短的没扩展过的点，所以这个点的距离永远不会再被改变，因而保证了算法的正确性。不过根据这个原理，用Dijkstra求最短路的图不能有负权边，因为扩展到负权边的时候会产生更短的距离，有可能就破坏了已经更新的点距离不会改变的性质。

小结

• 广度优先搜索用于在非加权图中查找最短路径。
• 狄克斯特拉算法用于在加权图中查找最短路径。
• 仅当权重为正时狄克斯特拉算法才管用。
• 如果图中包含负权边，使用贝尔曼-福特算法。

疑问

《算法图解》一书中说此算法只适用于有向无环图，正权边的有环图并不会影响已操作的节点的权重，为什么不适用？

书籍纠错

作者说他写错了，是适用于正权边的有环图的。 链接在此。